Today’s topics:
- A curious new geometric shape;
- The connections between math and literature;
- A new perhaps better map projection of the world

NY Times, Siobhan Roberts, 28 Mar 2023: Elusive ‘Einstein’ Solves a Longstanding Math Problem, subtitled “And it all began with a hobbyist ‘messing about and experimenting with shapes.'”
CNN, Jacopo Prisco, 6 Apr 2023: Newly discovered ‘einstein’ shape can do something no other tile can do
A geometry problem that has been puzzling scientists for 60 years has likely just been solved by an amateur mathematician with a newly discovered 13-sided shape.
Called “The hat” because it vaguely resembles a fedora, the elusive shape is an “einstein” (from the German “ein stein,” or “one stone”). That means it can completely cover a surface without ever creating a repeated pattern — something that had not yet been achieved with a single tile.
This story has been bouncing around the web for a couple weeks. It’s fascinating because it’s a sort of fundamental principle that has never been found before, and because it was found by an amateur hobbyist. Such discoveries are still possible even in the 21st century.
\\
NY Times, Sarah Hart guest essay, 7 Apr 2023: The Wondrous Connections Between Mathematics and Literature
The writer has a book on this topic, Once Upon a Prime: The Wondrous Connections Between Mathematics and Literature, coming out in a few days. I’ll have to read this one; it’s relevant to my interests. (Do you suppose she addresses anything science-fictional? No hint from the essay here that she might.)
Intrigued, I finally read “Moby-Dick,” and was delighted to find that it abounds with mathematical metaphors. I realized further it’s not just Herman Melville; Leo Tolstoy writes about calculus, James Joyce about geometry. Fractal structure underlies Michael Crichton’s “Jurassic Park” and algebraic principles govern various forms of poetry. We mathematicians even appear in work by authors as disparate as Arthur Conan Doyle and Chimamanda Ngozi Adichie.
Without using the term she evokes the Two Cultures divide in which “students are often forced to choose between studying either math and science or the humanities.” She concludes,
Great literature and great mathematics satisfy the same deep yearning in us: for beauty, for truth, for understanding. As the pioneering Russian mathematician Sofia Kovalevskaya wrote: “It is impossible to be a mathematician without being a poet in soul … the poet must see what others do not see, must see more deeply …. And the mathematician must do the same.”
By seeing mathematics and literature as part of the same quest — to understand the world and our place in it — we can add to our experience of both, and bring whole new layers of enjoyment to our favorite writing.
(Cue science fiction.)
\\\
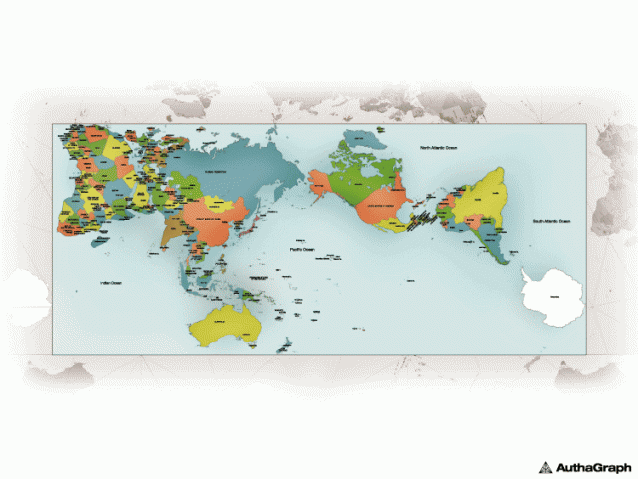
Discover, Nathanial Scharping, 29 Nov 2022 (originally from 2016): Finally, an Accurate World Map That Doesn’t Lie, subtitled “We’re long overdue for an accurate world map. Get the real story behind different map projections and see which one is the most accurate map of the world.”
I’ve written about map projections before. This piece has one I don’t think I’ve seen: the AuthaGraph world map. The article reviews the standard problem.
The standard classroom maps we all learned geography from are based on the Mercator projection, a 16th century rendering that preserved lines used for navigation while hideously distorting the true sizes of continents and oceans further from the equator. The result is a widespread misconception that Greenland is as big as Africa, Siberia and Canada are disproportionately massive, and that Antarctica apparently just goes on forever.
With an image of the Mercator projection.
Alas, the article does not mention my favorite projection, the Goode homolosine projection, which looks like the surface of the Earth torn apart like an orange peel, yet which maintains our intuitive positioning of the continents without too much distortion. Maybe I like it because one of my earliest atlases was a Goode’s World Atlas, with this projection on the cover….
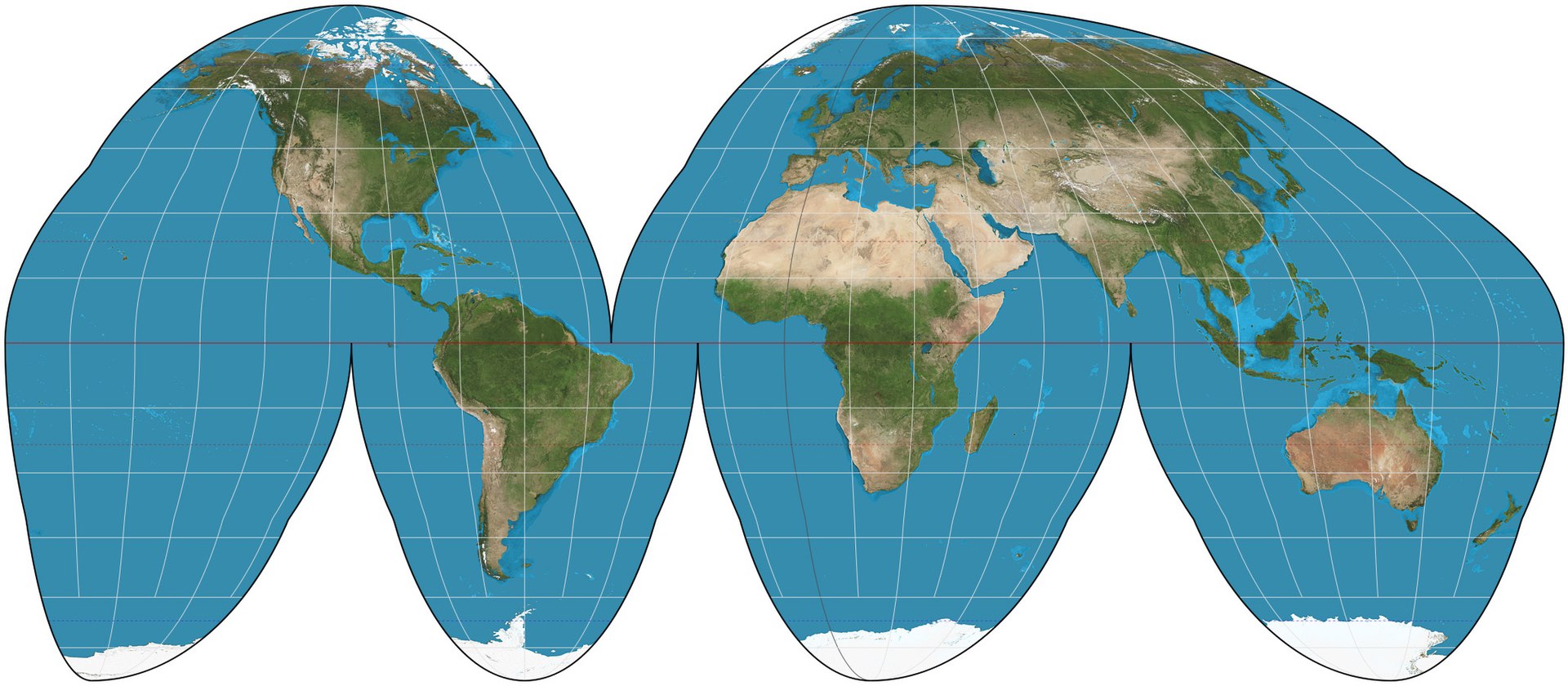
And of course, there are potentially many other projections, including those that don’t put north at the top; people in Australia likely don’t think of the world that way. And there are perspectives of the Earth, placing the center of the Pacific Ocean in the middle, that enforce the fact that most of our planet is covered by water.